Conclusions
Figure 7, Figues supplémentaires.
S24, S25, Vidéos supplémentaires S1–S3
visualiser notre nouveau modèle:
l’aboutissement d’un effort interdisciplinaire substantiel pour élucider le front du mécanisme d’Antikythera. Des recherches antérieures ont débloqué l’ingéniosité des Back Dials, nous montrons ici la richesse du Cosmos à l’avant.
Les principales caractéristiques structurelles de notre modèle sont prescrites par les preuves physiques, les principaux facteurs des relations de la période planétaire restaurées et la description de l’anneau dans la BCI.
Les fonctionnalités hypothétiques améliorent et justifient considérablement l’affichage Cosmos: un Dragon Hand relier thématiquement les cadrans avant et arrière; et un Système de lettres indexées pour les événements synodiques des planètes.
En raison de la perte de preuves, nous ne pouvons pas prétendre que notre modèle est une réplique de l’original, mais notre solution à ce puzzle 3D alambiqué puise un soutien puissant dans la logique de notre modèle et son adéquation exacte avec les preuves survivantes.
Le mécanisme d’Antikythera était un instrument informatique pour l’astronomie mathématique, incorporant des cycles de l’astronomie babylonienne et le flair grec pour la géométrie. Il a calculé le longitudes écliptiques de la Lune7, Soleil3 et planètes1,2,3,9,11; le phase de la Lunedix; le Âge de la lunedix; le phases synodiques des planètes; le jours exclus du calendrier métonique8; éclipses7,8,23— possibilités, fois, caractéristiques, années et saisons; le élévations et réglages héliacaux d’étoiles et de constellations proéminentes1,2,7,25; et le Cycle olympique8— un recueil astronomique grec ancien d’une ambition stupéfiante. Il s’agit du premier appareil connu qui a mécanisé les prédictions des théories scientifiques et il aurait pu automatiser de nombreux calculs nécessaires à sa propre conception ( Discussion supplémentaire S6) — les premières étapes de la mécanisation des mathématiques et des sciences. Notre travail révèle le mécanisme d’Antikythera comme une belle conception, traduite par une superbe ingénierie en un appareil de génie. Il remet en question toutes nos idées préconçues sur les capacités technologiques des anciens Grecs.
Source : Un modèle du cosmos dans le mécanisme antikythera grec ancien | Rapports scientifiques
- Article
- Accès ouvert
- Publié:
Un modèle du cosmos dans le mécanisme antikythera grec ancien
Rapports scientifiques volume 11, Numéro d’article: 5821 (2021)
Résumé
Le Mécanisme d’antikythera, une calculatrice astronomique grecque antique, a défié les chercheurs depuis sa découverte en 1901. Désormais divisé en 82 fragments, seul un tiers de l’original survit, dont 30 roues dentées en bronze corrodé. La tomodensitométrie à rayons X microfocus ( X-ray CT ) en 2005 a décodé la structure de l’arrière de la machine, mais l’avant est resté largement non résolu. La tomodensitométrie a également révélé des inscriptions décrivant les mouvements du Soleil, de la Lune et des cinq planètes connues dans l’Antiquité et comment elles étaient affichées à l’avant comme un cosmos grec ancien. Les inscriptions spécifiant des périodes planétaires complexes ont forcé une nouvelle réflexion sur la mécanisation de ce Cosmos, mais aucune reconstruction précédente n’a été proche de la correspondance des données. Nos découvertes conduisent à un nouveau modèle, satisfaisant et expliquant les preuves.La résolution de ce puzzle 3D complexe révèle une création de cycles de combinaison — de l’astronomie babylonienne, des mathématiques de l’Académie de Platon et des théories astronomiques grecques anciennes.
Introduction
Le mécanisme d’Antikythera est un trésor culturel qui a absorbé les chercheurs dans de nombreuses disciplines. C’était un ordinateur mécanique d’engrenages en bronze qui utilisait une technologie révolutionnaire pour faire des prédictions astronomiques, en mécanisant des cycles astronomiques et des théories1,2,3,4,5,6,7,8,9. Les principaux fragments survivants du mécanisme d’Antikythera sont étiquetés A – G et les fragments mineurs 1 – 757. Ils sont partiels, endommagés, corrodés et recouverts d’accrétions ( Fig. Supplémentaire. S1). Néanmoins, ils sont riches en preuves au niveau millimétrique — avec de beaux détails de composants mécaniques et des milliers de minuscules caractères de texte, enfouis à l’intérieur des fragments et non lus pendant plus de 2000 ans7. Le fragment A contient 27 des 30 vitesses survivantes, avec un seul rapport dans chacun des fragments B, C et D2,5,7,dix. Les fragments sont un puzzle 3D d’une grande complexité.
En 2005 Tomographie calculée par radiographie microfocus ( X-ray CT ) et Cartographie de texture polynomiale ( PTM ) des 82 fragments du mécanisme7 ajouté des données substantielles. Cela a conduit à une solution à l’arrière de la machine4,7,8,9, avec la découverte de la prédiction de l’éclipse et la mécanisation de l’anomalie lunaire7 ( Fig. Supplémentaire. S20). Le front est resté profondément controversé en raison de la perte de preuves matérielles.
De nombreuses tentatives infructueuses ont été faites pour concilier les preuves avec une exposition du cosmos grec ancien du soleil, de la lune et des cinq planètes connues dans l’Antiquité. En 1905 – 06, des notes de recherche remarquables de Rehm1 décrit Planétarium Mein, avec un affichage en anneau pour les planètes qui anticipe le modèle que nous présentons ici — mais mécaniquement complètement faux en raison de son manque de données ( Fig. Supplémentaire. S17). Dans le classique, Engrenages des Grecs2, Price a suggéré un engrenage perdu qui a calculé les mouvements planétaires, mais n’a fait aucune tentative de reconstruction. Ensuite, Wright a construit le premier système fonctionnel à l’avant qui calculait les mouvements et les périodes planétaires, avec un affichage du pointeur coaxial du Cosmos, prouvant sa faisabilité mécanique3 ( Fig. Supplémentaire. S18). Tentatives ultérieures de Freeth et Jones9 ( Fig. Supplémentaire. S19), et indépendamment par Carman, Thorndike et Evans11, a simplifié l’engrenage mais a été limité aux périodes de base pour les planètes. La plupart des reconstructions précédentes utilisaient des pointeurs pour les affichages planétaires, ce qui posait de graves problèmes de parallaxe3,9 et reflétant mal la description dans les inscriptions — voir la section sur Preuve inscriptive. Aucun de ces modèles ( Discussion supplémentaire S6) sont compatibles avec toutes les données actuellement connues.
Notre défi était de créer un nouveau modèle pour correspondre à toutes les preuves survivantes. Les caractéristiques de la roue motrice principale indiquent qu’elle a calculé des mouvements planétaires avec un système épicyclique complexe ( des engrenages montés sur d’autres engrenages ), mais sa conception est restée un mystère. La tomographie a révélé une multitude d’indices inattendus dans les inscriptions, décrivant un grec ancien Cosmos9 à l’avant, mais les tentatives de résoudre le système d’engrenage ne correspondaient pas à toutes les données1,2,3,6,9. Les preuves définissent un cadre pour un système épicyclique à l’avant9, mais les espaces disponibles pour les engrenages sont extrêmement limités. Il y avait également des composants inexpliqués dans le fragment D, révélés par le scanner à rayons X, et des difficultés techniques pour calculer la phase de la Lune9. Puis vint la découverte dans la tomographie de périodes étonnamment complexes pour les planètes Vénus et Saturne, rendant la tâche beaucoup plus difficile12.
Discussion et résultats
Nous voulions déterminer les cycles de tout les planètes de ce Cosmos ( pas seulement les cycles découverts pour Vénus et Saturne ); intégrer ces cycles dans des mécanismes hautement compacts, conformes aux preuves physiques; et de les entrelacer pour que leurs sorties correspondent à la ordre cosmologique coutumier ( CCO ), décrit ci-dessous. Nous montrons ici comment nous avons créé un engrenage et un affichage qui respecte les preuves inscriptives: un système d’anneaux avec neuf sorties —Lune, Nœuds, Mercure, Vénus, Soleil, Mars, Jupiter, Saturne et Date— transporté par des tubes imbriqués avec des bras supportant les anneaux. Le résultat est un nouveau modèle radical qui correspond à toutes les données et culmine dans un affichage élégant du cosmos grec ancien. Avec tant de manquants, nous garantissons l’intégrité de notre modèle avec un ensemble strict de Principes de reconstruction ( Discussion supplémentaire S1 ) et nous évaluons la force des données qui valident chaque élément — discuté dans le débat supplémentaire S1. La perte de preuves pourrait suggérer de nombreuses options pour un modèle. Ce qui nous a frappés avec force dans la fabrication du modèle actuel, c’est le peu de ces options: les contraintes créées par les preuves survivantes sont strictes et très difficiles à respecter.
Preuve inscriptive
La reconstruction du cosmos à l’avant du mécanisme d’Antikythera commence par l’analyse de quelques inscriptions remarquables. Figure 1 affiche les inscriptions de couverture avant et arrière ( FCI & BCI )9,12,13, qui sont essentiels pour comprendre ce cosmos. Pour l’analyse précédente13 et notre propre exploration ligne par ligne de la BCI, voir Discussion supplémentaire S2. Le BCI décrit l’affichage avant comme un Planétarium9,13: un Cosmos arrangé en anneaux, avec des planètes marquées par “ petites sphères ” et le soleil comme un “ petite sphère dorée ” avec “ ray ” et “ pointeur ” ( Fig. 1c, tableau supplémentaire S1, Figues supplémentaires. S2, S3). La FCI répertorie les cycles synodiques des planètes ( cycles relatif au soleil )12. Il s’agit d’une liste systématique, détaillant les événements synodiques et les intervalles en jours entre eux. Les planètes sont écrites dans le même ordre géocentrique que le BCI. Ajouter la lune et le soleil donne ordre cosmologique coutumier ( CCO ): Lune, Mercure, Vénus, Soleil, Mars, Jupiter, Saturne ( Fig. Supplémentaire. S4), dont les origines sont discutées dans le débat supplémentaire S2.
Inscriptions sur le mécanisme d’Antikythera. (un) COUVERTURE AVANT: cycles de la planète9,12, encadré par moulage à partir du fragment 3 ( Fig. Supplémentaire. S5). PLAQUE AVANT: Parapégma1,2,25, au-dessus et au-dessous de l’affichage cosmos, indexé sur le cadran du zodiaque. PLAQUE ARRIÈRE: Noms de mois sur le calendrier métonique4,8. Caractéristiques de l’éclipse, calendrier métonique rond et cadrans de prédiction de l’éclipse de Saros7,8— indexé sur ce dernier. Eclipse glyphes indexé sur le cadran Saros8. COUVERTURE DE RETOUR: Manuel de l’utilisateur, y compris la description du cosmos9,13 ( Discussion supplémentaire S2), structure du calendrier8 et Cycles Moon-Sun1,2. (b) Inscription sur la couverture avant ( FCI ): TDM composite à rayons X des fragments G, 26 et 29 et autres petits fragments9,12. La FCI décrit les cycles synodiques des planètes et est divisée en régions pour chaque planète dans le CCO ( Discussion supplémentaire S2). Les nombres ΥΞΒ ( 462 ) dans la section Vénus et ΥMΒ ( 442 ) dans la section Saturne sont mis en évidence12 ( Fig. Supplémentaire. S4). (c) Inscription au dos ( BCI )13 ( Discussion supplémentaire S2): TDM composite à rayons X des fragments A et B. A Manuel de l’utilisateur: la partie supérieure est une description de l’affichage avant du cosmos9 avec des planètes dans le CCO; en rouge sont les noms de planète ainsi que le mot KOΣMOY — “du Cosmos”.
Relations d’époque et théories grecques anciennes
Les anciens astronomes étaient fascinés par les mouvements des planètes. Comme on le voit sur Terre, ils présentent des inversions de mouvement périodiques contre les étoiles14. En astronomie babylonienne ces cycles synodiques étaient la base de la prédiction planétaire15, utilisant relations de période, tel que 5 cycles synodiques en 8 ans pour Vénus, que nous désignons par (5, 8). La FCI décrit événements synodiques, tel que points stationnaires, et des intervalles entre ces événements ( Fig. 1b, Fig. Supplémentaire. S4, Discussion supplémentaire S2).
Apollonios de Perga ( troisième-deuxième siècle avant JC ) a créé des théories épicycliques élégantes ( bien qu’inexactes ) pour expliquer ces mouvements anormaux comme la somme de deux mouvements circulaires uniformes, leurs périodes définies par des relations de période — le déférent et épicé modèles15 ( Discussion supplémentaire S3, Figues supplémentaires. S6, S7, S8). De telles théories étaient certainement utilisées dans le mécanisme d’Antikythera, étant donné que la Lune a été mécanisée en utilisant une théorie épicyclique similaire7. Le vrai soleil— le Soleil avec son mouvement variable — a également été expliqué dans la Grèce antique par des modèles épicycliques excentriques et équivalents14 ( Discussion supplémentaire S3).
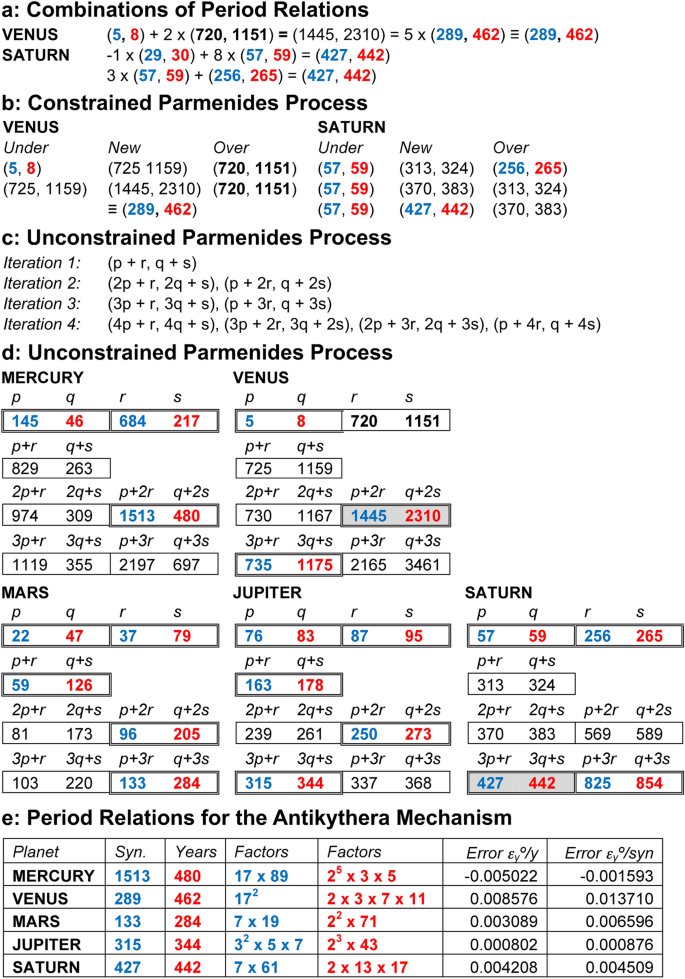
Les textes babyloniens énumèrent les périodes planétaires et leurs erreurs: périodes plus courtes et moins précises Textes de l’année de but ( GYT ) et des périodes plus longues et plus précises plus tard Textes cunéiformes astronomiques ( ACT )15 ( Tableaux supplémentaires S3, S4). Le GYT des périodes auraient pu être dérivées d’observations, mais pas plus ACTE périodes, telles que (720, 1151) pour Vénus ( Discussion supplémentaire S3). Pour comprendre quelles relations d’époque ont été intégrées au mécanisme d’Antikythera, le problème difficile était de découvrir leur dérivation. Pour Vénus, le designer d’origine a été confronté à un dilemme: la relation de période connue (5, 8) était très inexact, tandis que le précis (720, 1151) n’était pas mécanisable car 1151 est un nombre premier, nécessitant un équipement avec 1151 dents. Puis est venue une découverte notable en 2016 dans la FCI12: nombres inattendus ΥΞΒ (462) dans la section Vénus de la FCI et ΥMΒ (442) dans la section Saturne, se traduisant par des relations de période très précises: pour Vénus (289, 462) et Saturne (427, 442) ( Fig. 1b, Fig. Supplémentaire. S4). Surtout, ce sont factorisable, ce qui signifie qu’ils peuvent être mécanisés avec des engrenages de taille modérée, le nombre de dents incorporant les principaux facteurs des relations de période. Pour s’adapter à la géométrie du système épicyclique, les mécanismes doivent avoir des engrenages avec < 100 dents: les relations de période doivent avoir facteurs principaux < 100 ( Discussion supplémentaire S3. Il existe peu de relations de période aussi précises pour les planètes ( Tableaux supplémentaires S5, S6).
Le fait que les nouvelles relations de période pour Vénus et Saturne de la FCI soient factorisables renforce fortement l’idée qu’elles ont été incorporées dans les mécanismes planétaires du mécanisme d’Antikythera16. Les périodes pour les autres planètes sont illisibles ( dans les zones manquantes ou endommagées de la FCI ). Pour construire notre modèle, il était essentiel de découvrir les relations d’époque incarnées dans tous les mécanismes planétaires. Publications précédentes12,16 dérivé de la relation de la période de Vénus (289, 462) comme approximation itérative du babylonien connu (720, 1151Relation de période ), en utilisant un certain nombre de processus équivalents: fractions continues, anthyphairesis ou le Algorithme euclidien17,18. Pas de méthode similaire pour dériver le (427, 442On a pu trouver une relation de période ) pour Saturne, donc ce type d’approximation itérative n’était certainement pas le chemin vers les découvertes originales de ces périodes par les anciens Grecs.
Découverte de cycles dans le mécanisme d’Antikythera
Les périodes nouvellement découvertes pour Vénus et Saturne sont inconnues des études de l’astronomie babylonienne. Figure 2 explore comment ces périodes auraient pu être dérivées. Les indices provenaient de l’utilisation babylonienne de combinaisons linéaires de périodes conçues pour annuler les erreurs observées14. Figure 2a montre comment cela pourrait générer des périodes pour Vénus et Saturne, mais en choisissant les bonnes combinaisons linéaires essentiellement utilise les connaissances sur les erreurs dans les relations de période connues par rapport à la vraie valeur. L’absence de fines estimations d’erreurs de l’antiquité exclut ces méthodes pour notre modèle: des erreurs comme < 1 ° en 100 ans pour (720, 1151) dépassait l’astronomie à l’œil nu de l’époque hellénistique.
Trouver des relations de période. Les nombres bleus se réfèrent aux cycles synodiques; les nombres rouges se réfèrent aux années. Toutes les périodes de semences de ces processus sont connues des tables complémentaires d’astronomie babylonienne ( S5, S6). (un) Combinaisons linéaires de relations de la période babylonienne, qui donnent celles de Vénus et de Saturne de la FCI. (b) Relations de période générées par un conventionnel Processus de parménide, qui donne également ceux pour Vénus et Saturne de la FCI. (c) Itérations d’un Processus de parménide sans contrainte. ( 2p + 2r, 2q + 2 s ) est omis de l’itération 3 car il est identique à 2 x ( p + r, q + s ). (d) Trois itérations du Processus de parménide sans contrainte. Les paires de couleurs sont celles qui sont factorisables avec des facteurs premiers < 100. Les périodes gris-ombragé sont celles connues de la FCI. Notez que pour Vénus: (1445, 2310) ≡ (289, 462) et (735, 1175) ≡ (147, 235). Le même tableau avec des erreurs est indiqué dans le tableau supplémentaire S5. (e) Périodes dérivées du processus de parménide sans contrainte pour notre modèle du mécanisme d’antikythera et leurs erreurs, en utilisant nos trois critères de précision, factoriabilité et économie. À l’exception des périodes pour Vénus et Saturne, toutes les périodes finales étaient déjà connues en astronomie babylonienne. Les paramètres d’erreur sont définis dans la discussion supplémentaire S3.
Nous avons développé une nouvelle théorie sur la façon dont les périodes de Vénus et de Saturne ont été découvertes et l’appliquons pour restaurer les périodes planétaires manquantes. Un dialogue de Platon19 ( Ve-quatrième siècle avant JC ) a été nommé d’après le philosophe Parménide d’Elea ( sixième-cinquième siècle avant JC ). Ceci décrit Proposition de parménide17,18:
- En approximation θ, supposons rationnels, p / q et r / s, satisfaire p / q < θ < r / s.
- Puis (p + r) / (q + s) est une nouvelle estimation entre p / q et r / s:
- S’il s’agit d’une sous-estimation, c’est une meilleure sous-estimation que p / q.
- S’il s’agit d’une surestimation, c’est une meilleure surestimation que r / s.
En supposant qu’il s’agit d’une meilleure sous-estimation, l’étape suivante combine cela avec la surestimation originale pour créer ( p + 2r ) / ( q + 2s ). Ce serait testé contre q et le processus s’est répété. Ainsi, à partir de deux ratios de semences nous pouvons générer des combinaisons linéaires de plus en plus précises qui convergent vers θ. Le processus de Parménide est facilité et contraint par la connaissance de θ déterminer si chaque nouvelle estimation est une sous-estimation ou une surestimation. Figure 2b montre comment un conventionnel Processus de parménide peut générer nos périodes cibles, mais encore une fois, cela repose sur des connaissances indisponibles sur les erreurs. L’étape clé pour découvrir les cycles manquants est de modifier le Processus de parménide, il en est ainsi non contraint par connaissance d’erreurs — an Processus de parménide non contraint ( UPP ). Figure 2c, d montrent les combinaisons linéaires exhaustives qui sont systématiquement générées par ce processus. Comment choisir les relations de période adaptées à notre modèle? Deux critères ont sûrement été utilisés pour choisir les relations de période: précision et factoriabilité. La nécessité de monter les systèmes d’engrenage dans des espaces très serrés et le partage ingénieux des engrenages dans les trains d’engrenages survivants ( Fig. Supplémentaire. S20) inspire un troisième critère: économie— relations de période qui génèrent économique trains d’engrenages, utilisant engrenages partagés, calcul des cycles synodiques avec facteurs principaux partagés7 ( Discussions supplémentaires S3, S6).
Nous clarifions ici comment nous pensons que le processus a été utilisé. Le concepteur aurait généré des combinaisons linéaires à l’aide de l’UPP. À chaque étape, ces relations de période possibles auraient été examinées pour voir si elles répondaient aux critères du concepteur de précision, factoriabilité et économie. Factorizabilité aurait été un critère facile à évaluer. Précision est plus problématique, car nous ne pensons pas que les astronomes anciens avaient la capacité de faire des observations astronomiques très précises, comme en témoignent les enregistrements babyloniens ( Tableaux supplémentaires S3, S4). Économiedoit être examiné en relation avec les relations de période générées pour les autres planètes inférieures ou supérieures afin d’identifier les principaux facteurs partagés.
Vénus en est un bon exemple. Les anciens Babyloniens savaient que le (5, 8La période ) pour Vénus était très inexacte et ils avaient dérivé l’infactorisable (720, 1151) à partir de l’observation d’une erreur dans le cycle de 8 ans ( Discussion supplémentaire S3). De telles périodes étaient souvent décrites dans le monde antique comme des périodes exactes “ ”, bien que ce ne soit bien sûr pas le cas en termes modernes. Quand la période factorisable (289, 462) a été découvert à partir de l’UPP, il aurait été facile de calculer qu’il est en fait très proche de la période exacte “ ” (720, 1151). Ainsi, le concepteur aurait été convaincu que c’était une période précise. (289, 462) aurait alors été comparé à ( 1513, 480 ) pour Mercure de découvrir qu’ils partageaient le facteur commun 17 du nombre de cycles synodiques —, ce qui signifie qu’ils pouvaient être utilisés dans une conception à engrenages partagés pour satisfaire au critère de économie. Lorsque le concepteur avait découvert des relations d’époque qui correspondaient à tous les critères, le processus aurait été arrêté, car de nouvelles itérations auraient probablement conduit à des solutions de plus grande complexité.
L’UPP, combiné à nos trois critères, conduit à des dérivations remarquablement simples des relations entre Vénus et Saturne. Pour Vénus, Fig. 2d montre que la première relation de période factorisable est (1445, 2310) = 5 × (289, 462) ≡ (289, 462) = (172, 2 × 3 × 7 × 11), comme on le trouve dans la FCI. Pour Saturne, c’est (427, 442) = (7 × 61, 2 × 13 × 17), toujours de la FCI. Cette découverte permet des dérivations des périodes planétaires manquantes. Assurer notre troisième critère de économie, certains des principaux facteurs des cycles synodiques doivent être incorporés dans le premier engrenage fixe d’un train planétaire ( Discussion supplémentaire S4). Pour Mercure, nous recherchons un facteur de 17 dans le nombre de cycles synodiques à partager avec Vénus. La première itération factorisable est (1513, 480) = (17 × 89, 25 × 3 × 5) — partageant le facteur principal 17 avec (289, 462) pour Vénus — donc, un très bon choix. La multiplication par des entiers pour obtenir des engrenages viables conduit à des conceptions économiques avec un seul fixe 51-engrenage dentaire partagé entre Mercure et Vénus ( Fig. 3c, e )16. Pour les planètes supérieures, Mars et Jupiter, nous recherchons des périodes synodiques qui partagent le facteur 7 avec Saturne ( Fig. 3d, f ). Quelques itérations donnent des périodes synodiques appropriées — conduisant à des conceptions très économiques avec un 56-équipement fixe dentaire pour les trois planètes supérieures et le vrai soleil.
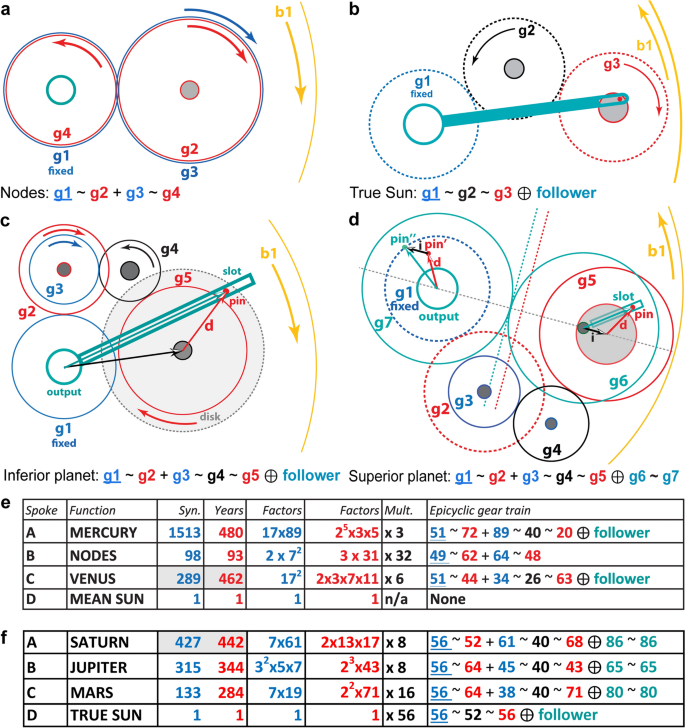
Mécanismes épicycliques pour le Cosmos. Les engrenages fixes sont soulignés; les engrenages bleus calculent les cycles synodiques; les engrenages rouges calculent les années; les engrenages noirs sont des engrenages plus inactifs: tous désignés par leur nombre de dents. “ ~ ” signifie “mailles avec”; “ + ” signifie “fixé au même tonneau”; “⊕” signifie “avec une broche et un suiveur, tournant sur l’axe central ” ou “ avec une broche et une fente sur des axes excentriques” — créant un mouvement variable ( turquoise ). Abonnés sont des tiges à fente qui suivent une broche sur le rapport épicyclique et tournent sur l’axe central. Pour chaque mécanisme, il y a un engrenage fixe au centre, emboutissant avec le premier engrenage épicyclique, qui est forcé de tourner par la rotation de b1 ou le CP. (un) Système épicyclique à 4 vitesses pour le Ligne de nœuds. (b) 3 vitesses modèle direct pour le vrai soleil. (c) 5 vitesses modèle direct pour une planète inférieure pour les relations de période complexes, avec un mouvement variable calculé par une broche et un abonné. (d) 7-engrenages modèle indirect pour une planète supérieure pour les relations de période complexes, avec un mouvement variable calculé par une broche et une fente sur des axes excentriques. (e) Relations de période et trains d’engrenages sur le Roue principale de conduite, b1; Part Mercure & Vénus fixe 51. (f) Relations de période et trains d’engrenages sur le Plaque circulaire, CP, partage fixe 56; engrenages également partagés entre Saturne / vrai Soleil et Mars / Jupiter ( Discussion supplémentaire S4).
Du tableau supplémentaire S5,S6, dans le débat supplémentaire S3 nous établissons que les périodes manquantes pour Mercure et Mars sont déterminées de manière unique par notre processus. Il existe deux options supplémentaires pour Jupiter qui partagent le nombre premier 7 dans le nombre de cycles synodiques ( Tableau supplémentaire S6 ). Dans une discussion supplémentaire S3 nous montrons comment l’un d’eux n’est pas possible et l’autre est très peu probable. L’UPP, combiné avec des critères de précision, factoriabilité et économie, explique les périodes de Vénus et de Saturne et ( presque ) génère uniquement les relations de période manquantes.
Mécanismes théoriques pour notre modèle
Le calcul de la position de la Lune dans le Zodiac et sa phase sont définis par des preuves physiques survivantes7,dix. Étant donné que les preuves manquent pour le Soleil et les planètes, nous devons développer des mécanismes théoriques, basés sur nos relations de période identifiées. Figure 3 montre des trains d’engrenages théoriques pour le soleil moyen, les nœuds et les planètes.
Paramètres géométriques des mécanismes planétaires de la Fig. 3c, d sont indiqués dans le tableau supplémentaire S9.
La façon dont le cadran Saros sur la plaque arrière prédit les éclipses implique essentiellement nœuds lunaires, mais ils ne sont pas décrits dans les inscriptions existantes. Avec leur rôle intégral dans les éclipses, un affichage des nœuds est une inclusion logique, unifiant les cadrans avant et arrière. Pour maximiser les informations affichées, nous avons créé un mécanisme pour une hypothétique Dragon Hand indiquer le Ligne de nœuds de la Lune, tel qu’inclus dans de nombreuses horloges astronomiques ultérieures20 ( Fig. Supplémentaire. S2). Nous devons souligner qu’il n’y a aucune preuve physique directe d’une indication de la ligne de nœuds de la lune. Nous avons ajouté cette fonctionnalité comme élément hypothétique pour les raisons thématiques déjà expliquées et parce qu’elle est facilement mécanisée avec une bonne précision avec un simple système épicyclique à 4 vitesses sur la colonne vertébrale B de b1. C’est une option intéressante à considérer pour le lecteur et elle coïncide avec l’ambition apparente du concepteur de créer un recueil astronomique, affichant la plupart des paramètres astronomiques qui préoccupaient l’astronomie hellénistique.
Tous les mécanismes Cosmos doivent être publiés dans le CCO, afin qu’ils soient cohérents avec la description dans le BCI. Au centre de ce Cosmos se trouve la Terre, puis la position de la Lune dans la phase zodiaque et lunaire. La position de la Lune est portée par la tonnelle centrale reliée au système épicyclique survivant ( ) qui calcule le mouvement variable de la Lune à l’arrière du mécanisme ( Fig. Supplémentaire. S1)7. Nous suivons la proposition initialedix pour le dispositif de phase de la Lune comme un simple différentiel, qui soustrait le mouvement du Soleil de celui de la Lune pour calculer la phase, affiché sur une petite sphère en noir et blanc.
Une rotation de pour la ligne de nœuds, dérivée des cycles métoniques et saros9, n’a pas pu être mécanisé à cause du grand nombre premier 223. Nous montrons qu’un ratio plus simple , avec une période plus précise de 18,6 ans14, peut être calculé par un train épicyclique à 4 vitesses ( Fig. 3a, Figues supplémentaires. S21, S22). Cela transforme un hypothétique double extrémité Dragon Hand20, dont la tête montre le nœud ascendant de la Lune et de la queue le nœud descendant.−12223−12223−593−593
En utilisant nos relations de période identifiées pour toutes les planètes, nous avons conçu de nouveaux mécanismes planétaires théoriques exprimant les théories épicycliques, qui correspondent aux preuves physiques. Pour les planètes inférieures, les mécanismes à 2 vitesses précédents3,9,21 sont inadéquats pour des relations de période plus complexes car les engrenages seraient trop gros. Des trains composés à deux étages avec des engrenages plus inactifs sont nécessaires, conduisant à de nouveaux mécanismes à 5 vitesses avec followers et fendus pour les mouvements variables7,9,21 ( Fig. 3c ). Pour les planètes supérieures, modèles antérieurs3,16 utilisé mécanismes directs, reflétant directement les théories épicycliques avec followers et fendus. Ici, nous proposons un roman 7 vitesses mécanismes indirects avec dispositifs à broches et à fentes7,9 pour mouvements variables ( Fig. 3d ), analogue au mécanisme subtil qui entraîne l’anomalie lunaire7. Par rapport à mécanismes directs, ceux-ci sont plus économiques; une meilleure adéquation aux preuves; et incorporer des relations de période exactement pour une plus grande précision. Les avantages cruciaux de mécanismes indirects sont élargis dans la discussion supplémentaire S4. Sans ces systèmes compacts qui peuvent tous être montés sur la même plaque, il aurait été impossible d’insérer l’engrenage dans les espaces disponibles. Preuves que les mécanismes de la Fig. 3 calculer correctement les théories épicycliques grecques anciennes sont incluses dans la discussion supplémentaire S4.
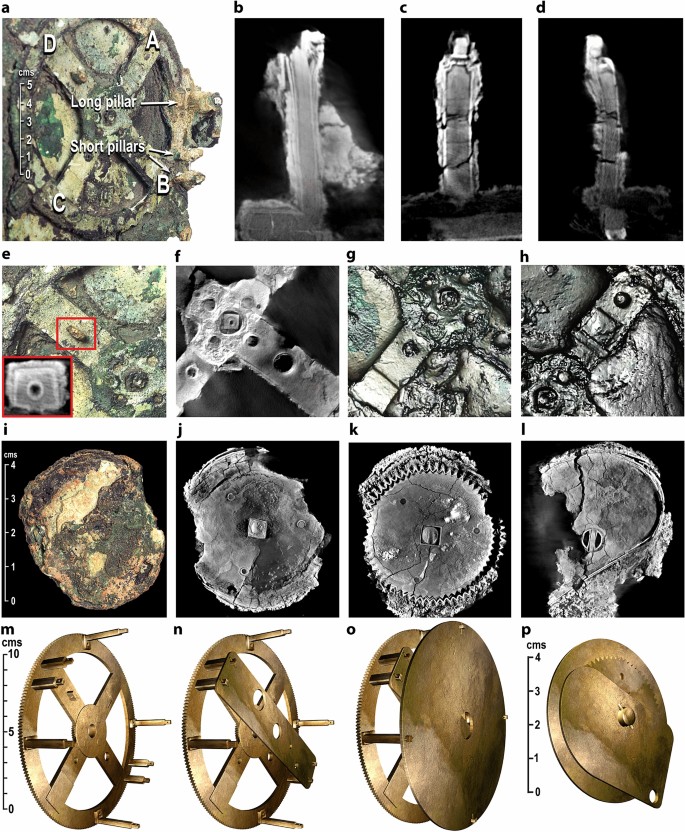
La question clé: pourrions-nous faire correspondre nos mécanismes théoriques aux données physiques? Fig. 4 montre certaines des preuves difficiles du fragment A7,22 ( Figues supplémentaires. S9, S10, S11, S12) et fragment D1,2,3,7,9 ( Figues supplémentaires. S13, S14). Tout modèle doit être cohérent avec ces données ( Discussion supplémentaire S5) ainsi que conforme aux principes horologiques / d’ingénierie du reste du mécanisme ( Figues supplémentaires. S15, S16).
Preuve de fragments A & D. Plaques et engrenages reconstruits. (un) Photographie du fragment A, montrant des piliers à la périphérie de b1 et fonctionnalités sur les rayons A, B, C, D. (b) TDM à rayons X du long pilier. (c–d) TDM à rayons X de courts piliers. (b–d) proviennent d’un volume de rayons X amélioré22. Tous les piliers ont des épaules et des extrémités percées. (e – h) Photographies, PTM, X-ray CT: caractéristiques des rayons D, B, C, A, y compris les trous, les dépressions circulaires et les zones aplaties. Dans (E), le bloc percé sur la rayons D est mis en évidence en rouge, avec un encart montrant une tranche de tomodensitométrie à rayons X à travers le bloc. (je–l) Photographie et tomodensitométrie à rayons X du fragment D, montrant un disque, engrenage et plaque. (m–o), Reconstruction informatique, montrant b1, Sangle sur les piliers courts; Plaque circulaire (CP) sur les longs piliers. (p) Reconstruction informatique des caractéristiques du fragment D, que nous reconstruisons en tant que composants épicycliques d’un mécanisme Vénus.
Fragment A: cadre essentiel pour la reconstruction
Le Roue principale de conduite, b1, a quatre rayons avec des trous proéminents, des zones aplaties et des piliers endommagés à sa périphérie ( Fig. 4a-h, figues supplémentaires. S11, S12) — preuve définitive d’un système épicyclique complexe1,2,3,9. Dans le mécanisme d’origine, il y avait quatre piliers courts et quatre longs avec des épaules et des trous pour les épingles de retenue, comme le montre la figure. 4a-d par les preuves de tomodensitométrie à rayons X. Ceux-ci impliquent que les piliers portaient des plaques: une plaque rectangulaire sur les piliers courts, le Sangle, et une plaque circulaire sur les longs piliers, le Plaque circulaire ( CP ) ( Fig. 4m-o )9. Ceci est le cadre essentiel pour toute reconstruction fidèle, les quatre rayons préconisant quatre fonctions différentes ( Fig. 4e-h ). Tout d’abord, nous reconstruisons les mécanismes entre b1 et le Sangle.
Fragment D: composants épicycliques pour le vénus
Figure 4i-l, Fig. Supplémentaire. S13 montrer les éléments cruciaux du fragment D. Études antérieures2,4,5 a suggéré qu’il y a deux vitesses dans le fragment D, mais c’est une illusion créée parce que la tonnelle s’est séparée7,9, tel qu’établi dans le débat supplémentaire S5 et Fig. Supplémentaire. S13. Le nombre de dents d’origine peut être déterminé de manière fiable comme 63 dents, étant donné que toutes les dents sauf trois survivent5,7,9. Les composants de base du fragment D sont un disque, engrenage et plaque, appelé ici le Plaque D, et un tonnelle reliant les trois éléments. Le disque et l’engrenage sont rivetés ensemble et ont des trous carrés au centre correspondant aux sections carrées à une extrémité de la tonnelle. À l’intérieur de l’épaisseur de l’engrenage, la tonnelle passe du carré au rond, où elle émerge dans la plaque. Sans espace pour aucun autre roulement sur cette tonnelle, il doit avoir pivoté dans la plaque D, qui sert également d’entretoise pour amener les composants épicycliques au bon niveau dans la hiérarchie de sortie et comme roulement pour un engrenage plus ralenti 26 dans le train de Vénus.
Aucun autre équipement survivant dans le mécanisme n’a un disque attaché. Dans un mécanisme de planète inférieur, le suiveur à broches et à fentes nécessite une broche attachée à l’engrenage épicyclique mais au-delà de son bord3,21: le disque attaché est de la bonne taille pour transporter la broche à la bonne distance du centre pour modéliser l’allongement maximal de Vénus. C’est sûrement l’épicycle de Vénus, comme suggéré précédemment9 et fortement renforcé ici. La largeur du Plaque D est proportionné à la largeur du Sangle, basé sur la séparation des piliers courts.
Mécanismes entre b1 et la sangle
Figure 5, Fig. Supplémentaire. S22 montrer comment le Soleil moyen, nœuds et planètes inférieures sont construits de manière complexe dans l’espace de 15,0 mm9 entre b1 et le Sangle en neuf couches étroitement remplies — correspondant aux preuves et à la densité de couche des engrenages survivants ( Figues supplémentaires. S16, S20, S21, Vidéo supplémentaire S1). Les mécanismes sont entrelacés de sorte que leurs tubes de sortie soient imbriqués dans le CCO, avec la sortie lunaire sur la tonnelle centrale.
Mécanismes entre b1 et la sangle. (un) Soleil moyen: Barre solaire moyenne attachée au bloc percé représentée sur la Fig. 4e; tube et équipement pour entrée dans le mécanisme de la phase de la Lune. (b) Nœuds: Mécanisme des engrenages de nœuds, roulement correspondant sur la Fig. 4f — train d’engrenages 49 ~ 62 + 64 ~ 48— avec tube de sortie et double extrémité Dragon Hand. (c) Vénus: Les engrenages de base du mécanisme de Vénus correspondent aux caractéristiques de la Fig. 4g. Train de vitesse 51 ~ 44 + 34 ~ 26 ~ 63— avec des composants du fragment D reconstruits sur la figure. 4p, plus tube de sortie et anneau Venus avec marqueur lapis-lazuli. Les engrenages épicycliques 26 ~ 63 pour Vénus, tournez la plaque D qui est attachée au sangle ( non représentée ). La fin du suiveur peut être vue derrière le disque. (d) Mercure: Les engrenages de base du mécanisme Mercury correspondent aux caractéristiques de la Fig. 4h. Train de vitesse 51 ~ 72 + 89 ~ 40 ~ 20— plus tube de sortie et anneau Mercury avec marqueur turquoise. Les engrenages épicycliques 40 ~ 20pour Mercure, tournez directement dans le sangle ( non illustré ). Le suiveur peut être vu derrière le côté gauche de l’anneau Mercury.
L’appareil de phase de lunedix a besoin d’accéder aux rotations lunaires et solaires adjacentes, car la phase est la différence entre ces rotations: un système de sortie d’anneau semble nécessiter le calcul de la vrai soleil deux fois9— une fois pour la saisie dans le Phase de lune et une fois pour le vrai soleil anneau, qui est la troisième sortie du système cyclique — donc séparé mécaniquement de la tonnelle lunaire centrale. Ici, nous résolvons ce problème clé avec un Soleil moyen sortie, alimentant le dispositif de phase de la Lune comme premier tube de sortie adjacent à la tonnelle lunaire centrale. b1 porte la rotation moyenne du soleil, mais il n’est pas possible de fixer une sortie moyenne du soleil en son centre car les vitesses centrales fixes empêchent cela: un accessoire à mi-chemin le long de la Spoke D est nécessaire pour combler les vitesses fixes. C’est pourquoi la sortie Sun moyenne est attachée via une barre au bloc percé précédemment mystérieux sur Spoke D ( Fig. 4e ). Cette idée importante permet un affichage en anneau pour le Cosmos, avec un seul vrai soleil sortie pour l’anneau solaire. La petite approximation inhérente à l’utilisation d’un Soleil moyen plutôt qu’un vrai soleil l’entrée dans la phase Lune est négligeable à l’échelle de la sphère de phase Lune de 6 mm de diamètre.
Il y a de grands avantages dans un système de sortie circulaire par opposition à un système de pointeur. Il coïncide beaucoup mieux avec la description de l’affichage de sortie dans le BCI. Il élimine la parallaxe sévère inhérente à un système de pointeur à neuf sorties. Il améliore considérablement les sorties astronomiques, en permettant aux phases synodiques des planètes d’être décrites par des inscriptions indexées, comme nous en discutons plus tard ( Fig. 8). Il conduit à un affichage robuste et élégant.
La correspondance étroite entre nos mécanismes proposés et les données est illustrée à la figure. 4. Les quatre rayons de b1 suggérer quatre fonctions différentes ( Fig. Supplémentaire. S12). Le Soleil moyen et les planètes inférieures en occupent trois. Quelle est la fonction de l’appui proéminent sur la Spoke B ( Fig. 4f )? Fig. 5b montre une solution: le roulement permet un système épicyclique à quatre vitesses qui calcule les nœuds lunaires. Notre nombre de dents proposé pour les engrenages et leurs modules ( Discussion supplémentaire S4) signifie que le roulement est exactement au bon endroit sur la fumée B. Aucune autre utilisation n’a été trouvée auparavant pour ce roulement.
Les déductions complexes qui conduisent à des reconstructions uniques des trains d’engrenages Venus & Mercury sont décrites dans la discussion supplémentaire S5. Nous soutenons que le fragment D comprend des composants épicycliques pour Vénus ( Fig. 4, Figues supplémentaires. S13, S14), que les trains d’engrenages suivent notre conception à 5 vitesses ( Fig. 3) et que tous doivent s’inscrire dans le cadre créé par les piliers ( Fig. 4). Les principaux facteurs des relations de période combinés aux preuves physiques déterminent ensuite les trains d’engrenages ( Fig. 3c, e, Fig. 4g, h, Fig. 5c, d ). En particulier, nous montrons que le sens astronomique de 63 est qu’il partage les nombres premiers 3 × 7 avec la relation de période pour Vénus, (289, 462) = (172, 2 × 3 × 7 × 11). Le Sangle est incliné aux rayons juste à l’angle correct de 11 ° pour accueillir les engrenages épicycliques de Mercure et Vénus — expliquant l’angle des piliers courts par rapport à b1. Pour la première fois, les fonctionnalités b1 et les composants du fragment D sont entièrement expliqués ( Fig. 4, 5, Fig. Supplémentaire. S21, Discussion supplémentaire S5, Vidéo supplémentaire S1). Nous concluons que nos trains d’engrenages Venus et Mercury sont fortement indiqué par la preuve.
Mécanismes entre la sangle et le CP
Il n’y a aucune preuve directe sur les systèmes d’engrenage qui ont calculé le vrai Soleil et les planètes supérieures. Cela signifie inévitablement des choix, bien que l’espace disponible limite fortement ces choix, car des systèmes très compacts sont nécessaires pour calculer les relations de période avancées. Figure 6a-e montre comment la plupart des engrenages pour le vrai Soleil et les planètes supérieures sont reconstruits dans l’espace de 9,7 mm entre les Sangle et le CP.
True Sun, planètes supérieures et engrenage cosmos explosé. (un) Les engrenages à l’avant du CP. Centre en ( a ): vitesse fixe 56, riveté sur une plaque subsidiaire ( non vu ). En bas à droite dans ( a ): 64, partagé entre Mars et Jupiter; En haut à gauche dans ( a ): 52, partagé entre le vrai soleil et Saturne. Laissé dans ( a ): 56 est l’équipement épicyclique du véritable engrenage solaire. (b) Les mécanismes vus de l’arrière du CP. Dans le sens des aiguilles d’une montre depuis le haut: Saturne, vrai soleil, Mars, Jupiter. (c) Gros plan du véritable mécanisme solaire. (d) Gros plan des engrenages montrant des couches entrelacées. (e) Gros plan des tubes de sortie. (f) Modèle éclaté d’engrenage cosmos. De droite à gauche: b1, Soleil moyen, Nœuds, Mercure, Vénus; vrai soleil et planètes supérieures engrenage; CP et engrenages partagés; Affichage de la bague; Dragon Hand; Position de la lune et mécanisme de phase.
Les vitesses initiales de ces systèmes sont devant le CP ( Fig. 6a ) — alléchant le problème d’espace et créant une conception mécanique robuste sans avoir besoin de supports pour prendre en charge les mécanismes comme dans un modèle précédent9. Un train fixe 56 au centre s’engage avec un train épicyclique composé sur le CP, calculant la rotation synodique du Soleil / planète par rapport au CP. Les tonnelles des trois engrenages 52, 56 et 64 passer par le CP pour conduire les mécanismes à l’arrière.
Les mécanismes sont disposés avec leurs sorties dans le CCO et sont alignés sur les axes cardinaux pour faciliter l’étalonnage. Les périodes planétaires et les trains d’engrenages sont répertoriés sur la figure. 3f et un diagramme schématique est illustré à la figure supplémentaire. S23. Étant donné que le nombre de dents doit inclure les principaux facteurs des relations de période, il existe peu d’options viables. Le vrai soleil mécanisme est un système simple à 3 vitesses, précédemment proposé3 ( Fig. 3b ), calcul de la théorie épicyclique grecque antique de la vrai soleil. Il partage le train fixe 56 avec toutes les planètes supérieures et il partage 52 avec le mécanisme Saturne. Par conséquent, il n’a besoin que d’un équipement supplémentaire 56. Les planètes supérieures, Mars, Jupiter et Saturne, sont disposées dans le sens horaire à partir du haut de la Fig. 6b. Tous leurs mécanismes partagent un équipement fixe 56 et suivez la même conception économique à 7 vitesses illustrée à la Fig. 3ré.
Le diagramme a explosé sur la Fig. 6f illustre comment tout le gearing Cosmos s’emboîte. Nous reconstruisons 34 vitesses devant b1 pour le système Cosmos. Les systèmes d’extension représentent 35 vitesses derrière b1 ( Tableau supplémentaire S8, Fig. Supplémentaire. S20)7— faisant un total de 69 vitesses ( Vidéos supplémentaires S2, S3). Le modèle suit tout notre Principes de reconstruction et matchs tout la preuve ( Discussion supplémentaire S1).
Affichage cosmos
Figure 7 combine nos découvertes actuelles en un élégant cosmos mécanique grec ancien à l’avant du mécanisme d’Antikythera.
Modèle informatique de l’affichage cosmos. Au centre, le dôme de la Terre, la phase de la Lune et sa position dans le Zodiaque — puis sonne pour Mercure, Vénus, vrai soleil, Mars, Jupiter, Saturne et Date, avec “ petite sphère ” marqueurs et marqueurs plus petits pour les oppositions. Marques à échelle et lettres d’index pour les cycles synodiques des planètes sont inscrits sur les anneaux de la planète. Entourant ceux-ci, le Zodiaque et le Calendrier égyptien2. Le vrai soleil anneau a un “ petite sphère dorée ” avec “ pointeur ”, comme décrit dans le BCI9. Lorsque les pointeurs Lune et Soleil coïncident, la sphère Lune montre le noir pour Nouvelle Lune; lorsque les pointeurs sont sur les côtés opposés, la sphère Lune montre le blanc pour Pleine Lunedix. Le Tête du Dragon Hand montre le nœud lunaire ascendant; le Queue le nœud descendant. Petits triangles sur le vrai soleil anneau, près du pointeur, affiche des limites d’éclipse plus larges et plus étroites. Des éclipses sont possibles si la main du dragon est dans ces limites. Quand le pointeur de la Lune est avant le Chef du dragon, la Lune est Sud du nœud; après, c’est Nord du nœud — à l’inverse pour le nœud descendant. A Date le pointeur est attaché à un anneau de date étroit, indiquant la date dans le calendrier égyptien2.
Les planètes sont identifiées par des pierres semi-précieuses sur des anneaux planétaires ( Figues supplémentaires. S3, S24, Discussion supplémentaire S6, Vidéos supplémentaires S1, S3). Un Âge de la lune échelle en jours3 sur le véritable anneau solaire est lu par le pointeur de la lune, faisant écho à la description de Cicéron du dispositif Archimède ( Discussion supplémentaire S2), “ … il était en fait vrai que la lune était toujours autant de révolutions derrière le soleil sur la finition en bronze que d’accord avec le nombre de jours qu’elle était derrière dans le ciel … ”.
La main du dragon indique des éclipses par sa proximité avec le vrai pointeur du soleil à la nouvelle ou à la pleine lune. Fermeture au nœud définit le schéma sophistiqué de prédiction des éclipses sur le mécanisme d’Antikythera8,23, avec limites symétriques pour les éclipses lunaires; et limites asymétriques pour les éclipses solaires, selon que la Lune est Nord ou Sud du nœud8,23. Ces limites plus larges et plus étroites sont indiquées par des triangles sur le véritable anneau solaire. Lorsque la main du dragon se trouve dans les limites pertinentes, une prédiction d’éclipse glyphe peut être trouvé sur le cadran Saros, avec des caractéristiques d’éclipse répertoriées dans les inscriptions d’éclipse8,23,24. Si la main du dragon est dans les limites plus larges, un saison des éclipses23 est en cours — se produisant deux fois chacun année de l’éclipse, montré par une rotation complète du Soleil par rapport à la Main Dragon. Comme Manuel de l’utilisateur, le BCI ( Fig. 1c ) peut avoir décrit ces fonctions dans la zone manquante au-dessus des planètes ( Fig. 1a ).
Indexation des événements synodiques aux anneaux planétaires
En règle générale, les inscriptions formelles et répétitives du mécanisme d’Antikythera sont indexées sur leurs cadrans: par exemple, Inscriptions de para-schémas au cadran du zodiaque1,2,7,25 et inscriptions d’éclipse au cadran Saros8,12,23. Pour chaque planète, ses événements synodiques —allongement maximum, points stationnaires, conjonctions et oppositions— se produit lorsque la planète est à un angle caractéristique du Soleil. En tournant le mécanisme, nous pouvons noter la position du soleil sur l’anneau de la planète pour chaque événement synodique ( Fig. 7). Nous proposons que les anneaux planétaires soient gravés de marques d’échelle pour ces événements lus par le pointeur Sun, avec lettres d’index à côté des marques d’échelle. Figure 8 montre comment les lettres d’index auraient référencé les événements formels et répétitifs de la FCI.
Système de lettre d’index hypothétique pour le FCI. La traduction provient d’une publication précédente12, où une transcription du texte grec original peut également être vue. Le schéma Index Letter est en rouge. L’ensemble du schéma utilise un seul alphabet grec de A à Ω, mais les premières lignes de Mercure manquent. Les données fragmentaires signifient qu’il existe encore de nombreuses incertitudes dans les lignes de texte.
Bien que ce schéma d’indexation ne soit pas prouvable, car le début des lignes est perdu ( Fig. 1b, Fig. Supplémentaire. S4), il est si logique d’améliorer l’astronomie sur l’écran cosmos et il s’adapte exactement à la structure ligne par ligne de la FCI. Il est frappant de constater que les événements synodiques de la FCI ne sont que ceux observables sur les anneaux planétaires: les apparences et disparitions habituelles des planètes sont omises, renforçant l’hypothèse d’indexation. Il est difficile de comprendre comment les informations de la FCI auraient pu être facilement accessibles par l’utilisateur sans un tel système d’indexation, ce qui justifie à son tour notre système de commandes.
La FCI9,12 énumère les intervalles en jours entre les événements synodiques — probablement calculés à partir des modèles épicycliques, pas les observations, car les intervalles réels sont si variables ( Fig. 1b ). La trigonométrie embryonnaire de l’époque hellénistique26 aurait rendu le calcul de ces éléments difficile. Nous proposons ici que le mécanisme d’Antikythera lui-même ait calculé ces intervalles synodiques en comptant les jours sur le Cadran de calendrier entre les événements synodiques indiqués par les marques d’échelle synodiques sur les anneaux planétaires — entièrement sans trigonométrie.
Conclusions
Figure 7, Figues supplémentaires. S24, S25, Vidéos supplémentaires S1–S3 visualiser notre nouveau modèle: l’aboutissement d’un effort interdisciplinaire substantiel pour élucider le front du mécanisme d’Antikythera. Des recherches antérieures ont débloqué l’ingéniosité des Back Dials, nous montrons ici la richesse du Cosmos à l’avant. Les principales caractéristiques structurelles de notre modèle sont prescrites par les preuves physiques, les principaux facteurs des relations de la période planétaire restaurées et la description de l’anneau dans la BCI. Les fonctionnalités hypothétiques améliorent et justifient considérablement l’affichage Cosmos: un Dragon Hand relier thématiquement les cadrans avant et arrière; et un Système de lettres indexéespour les événements synodiques des planètes.
En raison de la perte de preuves, nous ne pouvons pas prétendre que notre modèle est une réplique de l’original, mais notre solution à ce puzzle 3D alambiqué puise un soutien puissant dans la logique de notre modèle et son adéquation exacte avec les preuves survivantes. Le mécanisme d’Antikythera était un instrument informatique pour l’astronomie mathématique, incorporant des cycles de l’astronomie babylonienne et le flair grec pour la géométrie. Il a calculé le longitudes écliptiques de la Lune7, Soleil3 et planètes1,2,3,9,11; le phase de la Lunedix; le Âge de la lunedix; le phases synodiques des planètes; le jours exclus du calendrier métonique8; éclipses7,8,23— possibilités, fois, caractéristiques, années et saisons; le élévations et réglages héliacaux d’étoiles et de constellations proéminentes1,2,7,25; et le Cycle olympique8— un recueil astronomique grec ancien d’une ambition stupéfiante. Il s’agit du premier appareil connu qui a mécanisé les prédictions des théories scientifiques et il aurait pu automatiser de nombreux calculs nécessaires à sa propre conception ( Discussion supplémentaire S6) — les premières étapes de la mécanisation des mathématiques et des sciences. Notre travail révèle le mécanisme d’Antikythera comme une belle conception, traduite par une superbe ingénierie en un appareil de génie. Il remet en question toutes nos idées préconçues sur les capacités technologiques des anciens Grecs.
Méthodes
Les méthodes sont incorporées dans les informations supplémentaires.
Disponibilité des données
Les données qui soutiennent les résultats de cette étude sont disponibles auprès des auteurs correspondants sur demande raisonnable.
Changer l’historique
24 août 2021
Une correction à cet article a été publiée: https://doi.org/10.1038/s41598-021-96382-9
Références
-
Rehm, A. Notizbuch ( cahiers non publiés ), manuscrits de recherche et photographies de 1905 – 1906. Bayerische Staatsbibliothek, Munich, Allemagne. Rehmiana III / 7 et III / 9 ( 1905 – 1906 ).
-
Price, D. & de, S. Engrenages des Grecs: le mécanisme d’Antikythera — un ordinateur de calendrier de ca. 80 avant JC. American Philosophical Society. Trans. Suis. Philos. Soc. Nouveau serveur. 64, 1 – 70 ( Philadelphie ( 1974 ); réimprimé par Science History Publications, New York ) ( 1975 ).
-
Wright, M. T. Un affichage de planétarium pour le mécanisme d’Antikythera. Horol. J. 144( 5 ), 169 – 173 ( 2002 ).
-
Wright, M. T. Nombre de mois et d’années: le cadran arrière supérieur du mécanisme d’Antikythera. Bulletin de la Scientific Instrument Society, No. 87 ( 2005 ).
-
Wright, M. T. Le mécanisme d’Antikythera: un nouveau schéma d’engrenage. Bulletin de la Scientific Instrument Society, No. 85 ( 2005 ).
-
Wright, M. T. Engrenage épicyclique et mécanisme d’Antikythera, partie II. Horol antiquaire. 29( 2 ), 2005 ( 2005 ).
-
Freeth, T. et al. Décodage de la calculatrice astronomique grecque antique connue sous le nom de mécanisme Antikythera. Nature 444, 587 – 591 ( 2006 ).
-
Freeth, T., Jones, A., Steele, J. M. & Bitsakis, Y. Calendriers avec affichage Olympiade et prédiction d’éclipse sur le mécanisme Antikythera. Nature 454, 614 – 617 ( 2008 ).
-
Freeth, T. & Jones, A. Le cosmos dans le mécanisme d’Antikythera. ISAW Papers 4, février 2012. http://dlib.nyu.edu/awdl/isaw/isaw-papers/4/ ( 2012 ).
-
Wright, M. T. Le mécanisme d’Antikythera et l’historique précoce de l’affichage de la phase de lune. Horol antiquaire. 29, 319 – 329 ( 2006 ).
-
Carman, C., Thorndike, A. & Evans, J. Sur le dispositif à broches et à fentes du mécanisme d’Antikythera, avec une nouvelle application aux planètes supérieures. JAI 43, 93 – 116 ( 2012 ).
-
Anastasiou, M. et al. Les inscriptions du papier du mécanisme d’Antikythera 6: l’inscription sur la couverture avant. Almagest VII( 1 ), 250 – 297 ( 2016 ).
-
Bitsakis, Y. & Jones, A. Les inscriptions du papier du mécanisme d’Antikythera 5: l’inscription du couvercle arrière. Almagest VII( 1 ), 216 – 249 ( 2016 ).
-
Neugebauer, O. Une histoire de l’astronomie mathématique ancienne ( Springer, New York, 1975 ).
-
Neugebauer, O. Textes cunéiformes astronomiques, Vols I – III. 1ère édition, Lund Humphries London ( 1974 ). Réimprimé par Springer-Verlag ( 1983 ).
-
Wright, M. T. Le mécanisme d’Antikythera: trains d’engrenages composés pour les indications planétaires. Almagest. https://doi.org/10.1484/J.ALMAGEST.1.103717 ( 2013 ).
-
Fowler, D. H. Les mathématiques de l’Académie de Platon: une nouvelle reconstruction ( Clarendon Press, Oxford, 1987 ).
-
Fowler, D. H. Rapport dans les premières mathématiques grecques. Bull Am. Math. Soc. 1( 6 ), 807 – 846 ( 1979 ).
-
Lawlor, R. & Lawlor, D. Théon de Smyrne: mathématiques utiles pour comprendre Platon, III, 15, traduit de l’édition grecque / française de 1892 de J. Dupuis ( 1892 ).
-
Roi, H. C. & Millburn, J. R. À la hauteur des étoiles: l’évolution des planétariums ( Orréries et horloges astronomiques. Université de Toronto, Toronto Press, 1978 ).
-
Freeth, T. Le mécanisme d’Antikythera: 2 — Est-ce Posidonius ’ Orrery?. Méditer. Archaeol. Archaeom. 2( 2 ), 21 – 35 ( 2002 ).
-
Pakzad, A. et al. Amélioration de la reconstruction par tomodensitométrie aux rayons X du plus grand fragment du mécanisme d’Antikythera, une calculatrice astronomique grecque antique. PLoS ONE https://doi.org/10.1371/journal.pone.0207430 ( 2018 ).
-
Freeth, T. Eclipse prédiction sur la machine de calcul astronomique grecque antique connue sous le nom de mécanisme Antikythera. PLoS ONE https://doi.org/10.1371/journal.pone.0103275 ( 2014 ).
-
Anastasiou, M. et al. Les inscriptions du mécanisme d’Antikythera, papier 4: les inscriptions du cadran arrière et de la plaque arrière. Almagest 7( 1 ), 138 – 215 ( 2016 ).
-
Bitsakis, Y. & Jones, A. Les inscriptions du mécanisme d’Antikythera, papier 3: le cadran avant et les inscriptions de parapegma. Almagest VII( 1 ), 68 – 137 ( 2016 ).
-
Van Brummelen, G. Les mathématiques des cieux et de la terre: l’histoire ancienne de la trigonométrie ( Princeton, Princeton University Press, 2009 ).
Remerciements
Nous remercions University College London ( UCL ), Département de génie mécanique, d’avoir accueilli cette recherche. Nous reconnaissons avec gratitude le soutien de l’A. La Fondation G. Leventis et DH également de la Worshipful Company of Clockmakers. Nous apprécions la coopération et les installations de Charles Frodsham & Co., Chronometer, Watch & Clock makers. Nous sommes reconnaissants pour les conseils épigraphiques de S. Colvin ( UCL ), le soutien de W. Suen ( UCL ) et consultation avec C. Cullen ( Cambridge University ). Les données PTM sont publiées avec l’aimable autorisation de Hewlett-Packard et des données CT à rayons X gracieuseté de Nikon X-Tek Systems. Nous les remercions pour les autorisations d’utiliser les données. L’équipement prêté par X-Tek Systems a été utilisé pour collecter les données radiographiques. Pour la collecte de données de 2005, un grand merci à N.Kaltsas et son équipe de personnel et de conservateurs au Musée national d’archéologie d’Athènes, T. Malzbender et son équipe d’experts en imagerie de Hewlett-Packard, R. Hadland et son équipe de spécialistes des rayons X de X-Tek Systems et de l’équipe anglo-grecque de scientifiques, qui ont rendu cela possible. La collecte et l’analyse des données, dont dépend cette recherche actuelle, ont reçu un financement essentiel du Leverhulme Trust, du Walter Hudson Bequest, du comité de recherche de l’Université d’Athènes, la Fondation culturelle de la Banque nationale de Grèce, le J. F. Fondation Costopoulos et A. Fondation G. Leventis.dont dépend cette recherche actuelle, a reçu un financement essentiel du Leverhulme Trust, du Walter Hudson Bequest, du comité de recherche de l’Université d’Athènes, de la Fondation culturelle de la Banque nationale de Grèce, du J. F. Fondation Costopoulos et A. Fondation G. Leventis.dont dépend cette recherche actuelle, a reçu un financement essentiel du Leverhulme Trust, du Walter Hudson Bequest, du comité de recherche de l’Université d’Athènes, de la Fondation culturelle de la Banque nationale de Grèce, du J. F. Fondation Costopoulos et A. Fondation G. Leventis.
Déclarations d’éthique
Intérêts concurrents
Les auteurs ne déclarent aucun intérêt concurrentiel.
Informations supplémentaires
Note de l’éditeur
Springer Nature reste neutre en ce qui concerne les revendications de compétence dans les cartes publiées et les affiliations institutionnelles.
La version originale en ligne de cet article a été révisée: Cette version originale de cet article contenait des erreurs répétées, où le caractère grec Υ ( Upsilon ) a été incorrectement donné comme Ψ ( Psi ) et les fractions ont été incorrectement indiquées comme des exposants. Des modifications ont été apportées à la section “ Relations de la période et théories grecques anciennes ”, la légende de la figure 1, les mécanismes théoriques “ de notre section modèle ” et le fichier d’informations supplémentaires 4. Des informations complètes sur les corrections apportées se trouvent dans la correction pour cet article.
Informations supplémentaires
Informations supplémentaires 1.
Renseignements supplémentaires 2.
Renseignements supplémentaires 3.
Droits et autorisations
Accès libre Cet article est sous licence Creative Commons Attribution 4.0 International License, qui permet l’utilisation, le partage, l’adaptation, la distribution et la reproduction sur tout support ou format, tant que vous accordez un crédit approprié à l’auteur d’origine ( s ) et à la source, fournissez un lien vers la licence Creative Commons et indiquez si des modifications ont été apportées. Les images ou tout autre matériel tiers de cet article sont inclus dans la licence Creative Commons de l’article, sauf indication contraire dans une ligne de crédit du matériel. Si le matériel n’est pas inclus dans la licence Creative Commons de l’article et que votre utilisation prévue n’est pas autorisée par la réglementation légale ou dépasse l’utilisation autorisée, vous devrez obtenir l’autorisation directement du titulaire des droits d’auteur. Pour voir une copie de cette licence, visitez http://creativecommons.org/licenses/by/4.0/.